How a change in scale affects length, And Antica Farmacista

(sorry about this, but I've got to support myself somehow!)

The Antica Farmacista collection is sophistication and elegance in personal care and home fragrance. Refined and flawlessly crafted Antica Farmacista is a line that captures old-world European charm with unique fragrances and antique inspired apothecary bottles. Beautiful personal fragrances that last and last. Body care that soothes and pampers the skin and home ambiance diffusers that fill a room with tantalizing, fresh, warm, and comforting aromas for months of fragrant pleasure. Handsome packaging with an upscale look, Antica Farmacista is pure luxury in a bottle.

ANTICA FARMACISTA FOUND AT
WWW.YOUR-COSMETICS.COM

This is an applet that displays the relationship of velocity, acceleration and scale. It takes a bit to download, but it is worth it.

An experimenter is measuring the distance that an object moves. A second object, also moving, is used as a reference to measure the relative change in the position of the first. The top line, in applet 1, represents the path taken by the object to be observed and the bottom line represents the reference change in position or "clock".

you can use the applet to observe how the change in position of one object can be used to measure the change in position of another. Think of the bottom line as the ruler and the top line as the length to be measured. (For some browsers, you will need to click on the speed field and press the enter key to refresh the display (It seems that some events cause Java to toss the call stack.).) Use the check boxes to define the meaning of the adjacent numeric field. Check Acceleration and enter a value for a constant acceleration. Check the speed box if you want to explore a constant speed.

The following illustrates the relationship of scale to length, velocity and acceleration using the applet above.

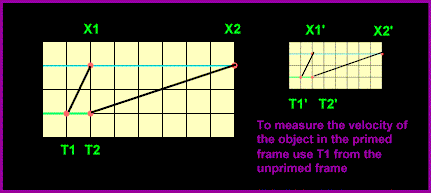With respect to frame 1 (to the right), X1 is the position of the object "when" the clock object is at T1 and X2 is its position when the clock object is at T2. Referring to Frame2, we use the same notation except that the coordinates have a ' after them. Note also that Frame 2 is an exact copy of Frame 1 in every respect except that it has been "compressed". In this case its linear density or scale, S, is twice that of Frame 1 (set the scale in the applet to 2 to create frame 2). We can represent this compressed "amount of space" as the product of the linear density and the measured (apparent) length. That is, the amount of space of a frame is conserved -- remains the same whether it is compressed or stretched. Makes sense, right?! (Kind of like a rubber band.) So then, here's the hard part. If you traverse the distance X1 or the X1' (shorter by 1/2), you will always traverse the same quantity of space.

The grid lines in frame 2 are shown to illustrate that it is a compressed version of frame 1. In reality, most objects (like space) do not have grid lines or rulers or clocks. Consequently, you will not be able to see any obvious compression in an object such as space or a brick of glass or lead. To measure distance, velocity or acceleration of any frame(E.g., a chicken or a toaster), you can only use conventional rulers and clocks, Consequently, to discover the scale of a an object (if such a property of a frame actually exists) you must measure its scale by an indirect method. To do this we examine the consequences of our development so far.

Note that as you compress a frame, the linear density or scale, S gets larger and L gets smaller. That is, the product , SL is constant. (See my paper for more details) Or:

This simply says that an amount of linear space in a frame for any measured length exists in other frames at other scales

If we knew nothing about Frame 2 (especially no grid lines), using our Frame 1 ruler and "clock" we would measure its velocity at X1' as:

And Since:

Then we have:

Or:

Then for acceleration in frame 1 we have:

And in Frame 2:

And since:

and

Then we have:

And finally...

Note that the above applet illustrates a growing length. In Relativity there is always a second and opposite perspective. E.g., object B moving with respect to object A is equivalent to object A moving with respect to object B, but the movement is in the opposite direction. In this example, imagine that the end of the top line is fixed to the display and that the frame is moving with respect to the other object (not the window). Why is this important?

The following applet presents two objects moving with respect to each other and the display. The velocity, acceleration and scale of the top object are controlled via the buttons and the numeric fields. As before, check the box for speed or acceleration to define the meaning of the number in the numeric field adjacent to the check boxes. The scale field defines the scale of the top object with respect to the bottom object. To amplify, imagine that the traveling squares below once had grid lines (like the graphs above) that you could use to determine the scale of the objects. Notice that as you decrease the scale of the object that its velocity increases.

Now try this: Set the velocity to 4 and leave the scale at 1. Note that for each unit traveled by the lower object that the upper object moves four units. I.e., the velocity of the upper object is (number of units traveled)/(number of units traveled by lower object). Now set the scale to 2. Now the upper object only moves 2 units per unit moved by the lower object (v=2 at this scale). But, note that the product of scale and velocity in the first case is 4 and in the second case is also 4. How does this work with acceleration? Try a couple of experiments with the above applet and see if the equations and experiment match.

Frame1 traveling with respect to a frame2 travels an amount of space equal to the scale of frame2 times the length of the path traveled, i.e., (Quantity of Space)=SL. Furthermore, if frame1 is moving with respect to frame2, then frame2 is moving with respect to frame1. This amount or quantity of space that an object travels is exactly the same for either frame.

When using coordinates to represent the motion of one frame with respect to a second frame, the motion of each with respect to the other is in an equal and exactly opposite direction. Consequently the sum of the quantities of space traveled by both frames is always 0.

How a change in scale affects length, velocity and acceleration