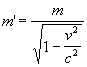Is Matter Shrinking?

It is often asked "If the space of the universe is expanding, and, if matter is mostly space, then isn’t matter expanding as well?". The conventional answer as well as my own is no. But, the explanation I have is much different than the answer you might read about in textbooks. See Do Atoms Get Bigger as the Universe Expands? for the textbook explanation.

Here is my side:

You are in deep space with a friend. You are facing each other. Neither one of you is aware of the very, very small rocket that I’ve placed on one of your space suits. After some random time interval, it fires. The acceleration from the rocket is very, very tiny, too small to be noticeable. Eventually you notice that your friend is moving away from you. But, to your friend, you are moving away. You might ask, who is actually receding from who?

This is the essential point of Galileo’s Relativity (Excellent link!), that the motion of an object can only be determined with respect to another object. (BTW, Einstein’s relativity does not replace Galileo’s. It extends it with a few new principles with some very dramatic consequences. )

Apply Galileo’s principle to galactic recession. From any point on our planet we can look in any direction into the universe and observe that all observable galaxies at distances greater than about 300 million light years look like they are receding from us. If you can see a galaxy moving away from our planet, you might conclude that, from the perspective of a viewer in one of these distant galaxies she must see you as moving away. If we can see all distant galaxies receding from us. then, according to Galileo’s principle, observers in these surrounding galaxies should see us as receding from them. That is, with respect to the rest of the universe we must be shrinking! Kind of weird huh? Well, lets call this the "shrinking matter hypothesis" and see if it makes sense.

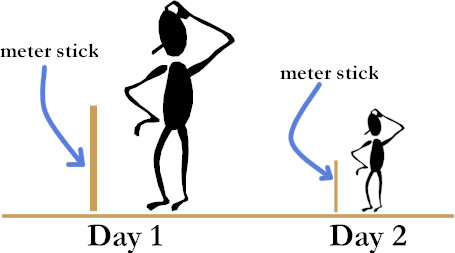
First, lets look at what must be your first question: "if we are shrinking, then how small can we get?" This is an easy question to answer, but not easy to understand.

Take a look around your surrounding environment, it is obvious to you that you and everything around you are not shrinking! But, how should your environment appear if it were shrinking?

Imagine that you are in the middle of a football stadium that is filled to capacity. You take a growing pill and start to slowly grow. To you, the stadium, the people and the whole earth will look as if they were shrinking. To the people in the stands, you will seem to be growing. Which is the true statement? Intuition says that the stadium and the people in it are not shrinking, only you are growing. But this leads to a contradiction of Galileo’s principle of relative motion. Furthermore, it violates one of Einstein’s principles that says "there are no favored frames." That is, according to Einstein’s principle, we can’t accept the view from one frame and reject the view from another.

Can we resolve these paradoxes? Sure! By allowing relative expansion. We don’t need to take a position with respect to the question. Both are correct! We can allow both interpretations! …How?

Think of distance as a measurement then look at your meter stick and consider the shrinking matter hypothesis. The distances that we are capable of measuring depend on the "length" of your material meter stick! That is, with respect to this piece of reference length we are not shrinking.

Say you are two meters tall on day 1 and on day 2 you are one meter tall. You shrink by a factor of two. So has the meter stick – since it too is made of matter. It is only one half of a meter on day 2. But is it? Clearly, since you and everything around you is made of matter (if matter is actually shrinking with respect to space) you would not be able to detect it – at least not with another piece of matter! So, maybe a meter doesn't become a one half a meter?

This raises an interesting question about a meter. How long is it? Really!? If it has shrunk, how long is it now?

This may be hard to believe, but, there is no "real" meter. A meter is just a definition. That is, when we define a unit length we always refer to (stand by) this definition even if it is shrinking (or growing) with respect to something else. This choice defines not only a physical frame of reference, but an intellectual one as well. That is, In order to be able to relate a "physical length" to an abstract length we require a "semantic alignment" that allows us to join physical reality to the power of mathematical abstraction. In some sense, with this union, we can translate the language of the universe into the language of mathematics.

With respect to our meter sticks, then the universe is growing. But, if we choose a couple of receding galaxies as the endpoints of our reference length, this length is by definition always a unit length and our material meter sticks are contracting. Physically, this is not a problem because all material proportions remain constant.

"Ok", you say, "but what about mass? If we are shrinking, shouldn’t we be getting less massive? Clearly we don’t see this!" Well if there were a geometric connection to mass then we might be able to use such a relationship to deduce how mass should change with respect to an expanding universe. As it turns out there is such a relationship that comes from Einstein’s special relativity:

Lets re-write these as:

This equation tells us that the product of length and mass (lm) for our material frame remains constant for all l’m’.  This means that if the length between two objects differs by some proportion a, then the mass of that object should differ by the proportion 1/a.  In otherwords, if a space is dense with respect to some reference length, then it will be more massive.

"Ah!" you say, "If we are talking about space where does mass enter the picture? Space is space and has nothing to do with mass!".

Actually, there are two very strong physical theories that suggest that space is filled with mass. The first is the theory about Zero Point Energy (you really should read this!). According to this theory, space is filled with energy. Consequently, if E=mc^2 then space is filled with mass.

The second theory is called the Cold Dark Matter hypothesis. It says that there are indications of unseen matter in the rotational behavior of galaxies. The observed rotational velocities of the arms of the galaxies cannot possibly rotate as fast as they do unless there is a gravitational source that we cannot yet explain. Otherwise, rotating galaxies as large as we have observed them would fly apart. A possible explanation is that there is matter in these galaxies that is not radiating any detectable radiation. Thus, it is assumed that if this matter exists, it is cold.

There is a third theory, (my own) that equates mass to the scale of a frame of reference. I call this theory a Deeply Unified Field Theory since it unifies the units of measurement rather than the four fundamental forces. The motivation for this theory is to explain the relationship of mass to field. Unifying the four fundamental forces (the holy grail of physics) seems an impossible task if we don’t understand the fundamental significance (via first principles) of f=ma (force), p=mv (momentum) or E=mc^2. However, when we consider how length, and especially a reference length is contracting or expanding, it seems very rational to examine the scale of one reference length with respect to any other. In my work, in the cases that I have considered so far, the scale of a frame appears in the same place and in the same way as mass does in some of the most fundamental equations known to physics.

Now, what about time? The same equations apply to time. That is, for time we have.

Apparently, even though the universe is expanding (or matter is contracting) the effects are not easily detected -- locally.  But then, so many things in physics depend on some kind of a change or a difference – energy, field, work, motion etc.. And, in our universe, we can see a difference in the expansion of space and/or the contraction of matter. Might there be physical effects that we be could detect? (Ans: yes!)

Einstein found that if he represented space as a curved space in four dimensions that he could calculate a field potential. The form of his field equation matched Newton’s gravitational field exactly. That is, he found that space itself can account for gravity – a causal effect! So then, if a curved space can have a causal effect, what effects, other than a Doppler shift, might we be able to detect as a result of an expanding space?

A question for the Experts: Consider equation 1.  If you were to look at meter stick in your hand, how would you know if it was contracted with respect to any other length in the universe or not?  If you measured it with another meter stick, you'd learn nothing.  (That would be like looking at your hand to find out how fast you were going.)

A question for the layman: Recently, astronomers have found that, not only is the universe expanding (But wait! There is no "outside" of the universe!), the rate of expansion is accelerating.  Now, if we choose two distant galaxies as our reference length, then not only is matter shrinking with respect to this reference, its rate of shrinkage should be accelerating.  Whenever an object accelerates there is an associated force.... 
Can we detect the expanding universe locally?  Have you ever seen an apple fall to the earth?

Chase, Scott I., "What is Dark Matter?" (updated 11-MAY-1993), http://math.ucr.edu/home/baez/physics/dark_matter.html

Puthoff, H. E.   "Quantum Vacuum Fluctuations: A New Rosetta Stone of Physics?",  http://www.best.com/~dolphin/zpe.html

THE CLASSICAL VACUUM [ZERO-POINT ENERGY] From Scientific American Magazine, Aug. 1985, pp 70-78. http://www.padrak.com/ine/ZPESCIAM2.html

Weiss, Michael "What Causes the Hubble Redshift? Are the Light-Waves "Stretched" as the Universe Expands, or is the Light Doppler-Shifted Because Distant Galaxies are Moving Away From Us?", 1994,  http://math.ucr.edu/home/baez/physics/hubble.html

Element Skateboards, Completes, Decks, Wheels and more 4-less!
4-SkateBoards.com