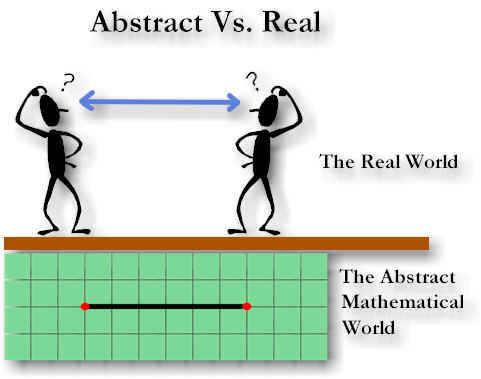
Let's just say you and God made a deal to remove all matter from the universe so that you could measure empty space.   What questions might you have about a distance say from point A to point B.   You might ask, for example, how many meters there are between point A and point B.  But, what in the universe would you choose to define a meter?  In an empty universe there is nothing you can point to and say "that is my unit length and it is one meter long.".  What you might do, however, is simply define the distance between A and B as one unit length.  If you can define a meter stick for a reference length, why not the AB distance.  A definition is an abstraction, why not choose a unit of space as an abstract ruler.  Actually, if you can figure out a way to use empty space as a ruler, then you've got a way of measuring space with space.   This would be far better than measuring a spatial distance with a material object (a meter stick).  After all, a material unit length, like a meter, is based on matter.  And, if space is expanding (or matter is contracting (see "Is Matter Shrinking")) we might want to consider that expanding spatial coordinates will drift relative to our material coordinates.  And, we might be very interested in the physical consequences of these drifting coordinates in a more general context.  Anyway, back to my point...(more on this later...)  In this experiment there is nothing except empty space.  There is nothing we can measure the velocity, or acceleration of.  No photons so there is no light.  There's no mass or energy.  In an empty universe, there is nothing for us to sense at all!   This situation is kind of like the question "if a tree falls in the forest and there is no one there to hear it, does it make a sound?"  Actually, the idea of an empty space or a universe with no matter or energy may not even be conceptually possible.  Of Einstein's last writings, one of the things he said is "there is no space without field" (the Forward in Max Jammer's "Concepts of Space").   Of course the only fields we know of are material fields.  So if we are to have the situation of an "empty universe" it would have to be just one particle with a field.  That is, this one existent would be (not represent) the entire universe.   But, then we have another "tree in the forest" kind of situation.  If this is the only particle/field in the universe, can we really say that there is a field (and thus space) if it has nothing to act on?  And should we even consider this case?... it seems like a waste of time.  Patience..., there are a couple of more questions to ask.  The first is, if this is the only existent there is, can it move?  Can it rotate?  Not if Gallileo was right.  If motion occurs only with respect to another object, then this one existent universe cannot go anywhere.  If you think about it it makes sense.  There is nothing outside of the universe for our single existent to move through (like space) and no markers staked to the "outside (or inside) of the universe" that would allow us to show "the universe had rotated".  It might seem that there is not a lot we can say about a one particle universe.  Except that you can say "there's not a lot we can say about a one particle universe".  Actually there is one more thing that we can say.  A one particle universe has no center.  This probably seems pretty strange, but to show that this particle surrounded by field was at the center of the universe we would have to show that there was something we could call a boundary which was a constant distance away from the particle for all angles.  We can't do this.   Why?  Well, first look at the universe as a venn diagram:

The blue represents everything that exists and the black represents everything that does not exist.  Of course there are no non-existents.  There is nothing that we could imagine that could actually provide a border for existence itself.   So the black part, although I have represented it as a non-existence, is not there (well, maybe unicorns and dragons).  In a logical sense, there is nothing outside of existence.  The definition of "center" depends on a boundary equidistant from the "center".   No boundary, no center.

OK.  We'd like to measure the field strength of this one particle.   If we could show that the field strength was the same for each constant r from a hypothetical center we would have something we could define as a "boundary".  Then we might infer that our particle was at the center of the universe.  So lets add a second particle -- a test particle.  Lets call our first particle A and our new particle B.   If the particle B moves toward particle A then we have an attractive force.   If they move away from each other then we have a repulsive force.  But we have another problem.  How can we tell if there is motion between these two particles at all if there is no reference object to compare the distance between A and B against?   This might seem kind of confusing.   Gallileo taught us that motion can and does only occur with respect to another object.  Here we have two objects.   According to Gallileo, motion should be possible.   Why can't we say that they are moving with respect to each other? 

We can certainly imagine that these two particles might be surrounded by some kind of field and move toward each other under, say, gravitational attraction.  To talk about a physical change in position we need to express this physical change in physical units (to avoid defining nature) so we must have a ruler (like Gallileo had) to define a static distance.  Without something physical that establishes physical "staticness" and physical "lengthness" we have no criteria to judge what kind of distance or motion we are "observing".  So, to define our ruler, we add two more points/particles.   Call these C and D and let these define the endpoints of our ruler.  As we've seen before (in "Is Matter Shrinking") you can define any two particles to represent the endpoints of a static reference length.  Not only does it define "length" it also defines "static" and "static" implicitly defines "dynamic".   These might seem like trivial semantic details.  And they are.  But with these "observational semantics" we can find the equivalent "theoretical semantics" -- the math.  And math is what gives a theory its power.

Now, let's choose C and D as our reference length and call the distance between C and D l₀.  Note that however close or far apart we might imagine C is from D it is still a unit length (Notice that coincidence is not possible! Can you measure precisely without coincidence?... Food for thought...).   Keep in mind that a unit length is a just mathematical notion.  It is a conceptual piece of how we represent the physical.  That is, it's part of a conceptual technique that helps us represent the universe.   (remember, a unit length is not real, its just a definition.  Face north say it three times then face east say it three times again... )

Let's use our ruler to measure the distance from point A to point B.   Since our ruler defines physical "staticness" and "lengthness" we have an enormous body of knowledge we can apply to the physical.   Mathtematical science...  And in particular, geometry.  But to actually be able to apply geometry to our two "lengths" we need a way of using them to construct numbers -- or variables!.  And that is just what a measurement does.   In, physics this is one of the most important steps.  It is what gives a theory what physicists call "physical significance".  So lets take a minute and look at how we turn a length into a number.

The Measuring process

Measuring the length of somthing is something we've all done.  But no one really looks too closely at the role of the ruler in the measuring process.  It works fairly well just as we've been using it for the last couple of thousand years.   But what we've found in studying quantum mechanics is that it seems imposible, even in theory, to get the exact measurements we expect.  Why?... We tend to think of a unit of length like we think of single marble, or a chicken.  We can identify objects, like marbles, and count them exactly.  In the universe, however, if we look for a "true" reference unit length, we find that there are an infinite number of choices.  We do not find any single one that somehow identifies itself as the one single "true" unit of length.  In other words, length, in a natural sense, is fundamentally ambigous.  Whereas unit has  both a natural and sythetic exactness.  If you have a philosopical bent, you might ask yourself "Why do I need a reference length to quantify a length but I don't need a reference chicken to count chickens".

We want to acheive, in a measurement, the same exactness that you get from counting.   The property that gives a count its exactness is that objects (like chickens or marbles) have a unique and unambigous identity (a physical uniqueness).  If we assign a number to a length we give the length a mathematical identity.  The way we do this is to find the number of reference objects in the target. 

Lets start with two sticks call them r₁ and r₀.   We'll define r₀ as the ruler length and r₁ as the target -- the length we will translate into a number.  We use the following algorithm to measure (construct a number):

Notice there is no placement of the decimal point.  Why?   Because we don't really know if r₀ represents a legnth that is 1.0 units long (it could be compressed -- how would you know?).  Although it is a reference length we have not yet assigned it a numerical identity (...and may not want to!).  We can choose any number we want to.  Note that where we place the decimal point would depend on this choice.  To amend our algorithm then, lets say that at the top of our algorithm we define our reference length to represent 1.0 units.  Then the first time we have to break r₀ we place a decimal point to the right of the accumulated digits and after we append the zero.

There are short-cuts we can take.  You probably already know them.  You've probably never broken a ruler or the thing you were measuring -- probably because you've never had to write a measuring algorithm yourself.  I've broken lengths off because that is effectively what we do when we measure things.  As we look at greater and greater precission we ignore the results of our previous observations as we attend to the smaller and smaller fractions and build greater and greater precission.  The salient point, however, is that this algorithm sets up another view of a measurement that allows us to express a measurement in another way.  Notice that by breaking fragments off of r₁ we are physically subtracting r₀ from r₁.  There is a mathematical shortcut we can use to represent an iterative subtraction: division.   In fact we can replace our measuring algorithm entirely with the mathematical equivalent:

Why is this good?  Well, it emphasizes the conceptual dependancy of Mathematical length on a reference object -- something that must exist.    That is, without a Ruler we don't have a Length.  Length in not an intrinsic property of matter -- its one of our inventions.  And secondly, this makes Length physically significant -- i.e., relating a length (an abstraction) to a physical object which implyies physical properties.  This is an important property to establish in the begining of a physical theory.   The third property is that equation (1) is abstract.   That is, it may be generalized for many kinds of measurements.  With respect to length there is one big problem though.  If Target and Ruler are shrinking with respect to some frame in exactly the same proportion Length will remain constant (take a look around you) in some frames and change with respect to others.    The quality of the number we get as a length just does not compare to a count of marbles.  It doesn't matter if you are growing or shrinking, the number of marbles in a bowl will always be the same number.   Whereas if I see a length that is shrinking with a rate v, observers of the shrinking frame will say it is always a constant x.  While we can accomodate this situation in a general way and for all observers, the math turns out to be surprizingly difficult.

There is an alternative way, it turns out, of representing length that is quite simple, frame independent and entails probably the most useful application of equation 1.   That is, measuring one ruler with another.

First, consider the  "shrinking matter hypothesis".   If it's valid, then our material rulers have shrunk with respect to the universe.    Or put another way, the space represented by our material rulers might be denser than that of inter-galactic space.  To test this idea, we can use our measurement expression to measure this spatial density or scale as:

This kind of scale is similar to the conversion constants you use to convert feet to meters or cubits.  There is an important distinction here, however, in that our ruler is exactly analogous to a geometric line -- something bounded by exactly two points.  A meterstick, made out of metal or wood, has zillions and zillions of "points" (particles) between its "endpoints".  While a conventional ruler is similar to a line it does not fit the exact definition of a geometric line.

Take the measurement of a ruler of frame x with respect to frame x':